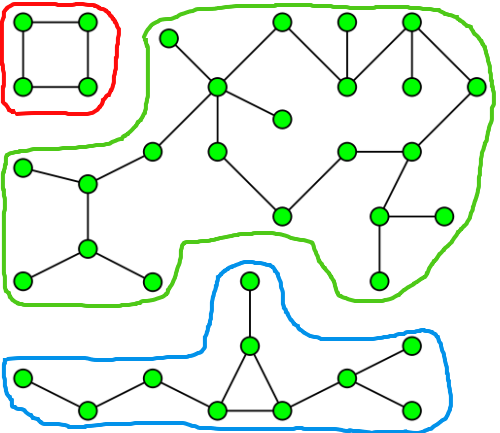
在 LeetCode 上练习时了解到,并查集 这一数据结构比较常用于解决图论方面的问题,其应用场景与搜索有很多重叠。例如,两者都可用于求无向图中连通分量 (connected component or just component)的个数。下图1中就有三个连通分量,分别以不同颜色标出:
LeetCode 例题:547. 省份数量
并查集
鉴于 STL 没有实现并查集(已知 Boost
有),我们需要自己动手实现:以 vector<int> 为本体,辅以 get_root() 和 merge_set() 两个函数,即可完成。注意,此实现舍弃了性能的完整性2,追求的目标是代码量小、功能够用,适用于做题和笔试场景。
值得注意的有两点:
- 路径压缩(path compression)的实现方式
- 如何清点当前并查集中集合的数量
1class Solution {
2 int get_root(vector<int> &unionset, int idx) {
3 if (idx == unionset[idx]) {
4 return idx;
5 } else {
6 return unionset[idx] = get_root(unionset, unionset[idx]); // KEY!!! This is how parents are updated
7 // from intermediate nodes to root (path compression)
8 }
9 }
10 void merge_set(vector<int> &unionset, int a, int b) {
11 unionset[get_root(unionset, a)] = get_root(unionset, b);
12 }
13public:
14 int findCircleNum(vector<vector<int>>& M) {
15 const int N = M.size();
16 vector<int> unionset(N);
17 for (int i = 0; i < N; ++i) {
18 unionset[i] = i;
19 }
20 for (int i = 1; i < N; ++i) {
21 for (int j = 0; j < i; ++j) {
22 if (M[i][j]) {
23 merge_set(unionset, i, j);
24 }
25 }
26 }
27
28 /////////////////////////////////////////////// this part
29 // vector<int> has(N, 0);
30 // for (int i = 0; i < unionset.size(); ++i) {
31 // has[get_root(unionset, i)] = 1;
32 // }
33 // int sum = 0;
34 // for (int i = 0; i < has.size(); ++i) {
35 // sum += has[i];
36 // }
37 // return sum;
38 /////////////////////////////////////////////// can be improved as follows
39 /////////////////////////////////////////////// (check # of roots in the union set):
40 int num = 0;
41 for (int i = 0; i < N; ++i) {
42 if (unionset[i] == i) {
43 num++;
44 }
45 }
46 return num;
47 ///////////////////////////////////////////////
48 }
49};
深搜
1class Solution {
2public:
3 int findCircleNum(vector<vector<int>>& M) {
4 const int N = M.size();
5 vector<bool> visited(N, false);
6 int count = 0;
7 stack<int> s;
8 for (int i = 0; i < N; i++) {
9 if (visited[i]) {
10 continue;
11 }
12 visited[i] = true;
13 s.push(i);
14 while (!s.empty()) {
15 int pivot = s.top();
16 s.pop();
17 for (int j = 0; j < N; ++j) {
18 if (M[pivot][j] && !visited[j]) {
19 visited[j] = true;
20 s.push(j);
21 }
22 }
23 }
24 count++;
25 }
26 return count;
27 }
28};
深搜之数据结构选配:
- 记录节点已被遍历的 visited 数组:
vector<bool> visited(N, false) - 维护深搜遍历顺序的栈:
stack<int> s
广搜
1class Solution {
2public:
3 int findCircleNum(vector<vector<int>>& M) {
4 const int N = M.size();
5 vector<bool> visited(N, false);
6 queue<int> q;
7 int count = 0;
8 for (int i = 0; i < N; ++i) {
9 if (visited[i]) {
10 continue;
11 }
12 visited[i] = true;
13 q.push(i);
14 while (!q.empty()) {
15 int n = q.front();
16 q.pop();
17 for (int j = 0; j < N; ++j) {
18 if (!visited[j] && M[n][j]) {
19 visited[j] = true;
20 q.push(j);
21 }
22 }
23 }
24 count++;
25 }
26 return count;
27 }
28};
广搜之数据结构选配:
- 记录节点已被遍历的 visited 数组:
vector<bool> visited(N, false) - 维护广搜遍历顺序的队列:
queue<int> q
注意:当有用到 visited 数组时,要考虑清楚 visited 置位的时机。一个节点“be visited”,应该被定义为“被发现”(已经经由其他节点探知),还是“被处理”(刚从栈顶/队头弹出,当前正在处理)?此例题中,“be visited”被定义为了“被发现”。

